Teorema binomial
Dalam aljabar elementer,
teorema binomial adalah teorema yang menjelaskan mengenai pengembangan eksponen dari penjumlahan antara dua
variabel (binomial). Berdasarkan
teorema ini, dimungkinkan untuk mengembangkan eksponen (
x +
y)
n menjadi sebuah penjumlahan dari suku-suku dengan bentuk
axbyc, dimana
eksponen b dan
c adalah bilangan bulat non negatif dengan
b + c = n, dan koefisien
a dari setiap suku adalah bilangan bulat positif tertentu tergantung pada
n dan
b. Ketika suatu eksponen adalah nol, faktor yang bereksponen nol tersebut biasanya dihilangkan dari sukunya. Contohnya,


Koefisien a pada suku axbyc dikenal sebagai koefisien binomial 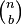 atau
atau  (keduanya memiliki nilai yang sama). Koefisien untuk setiap variasi n dan b dapat disusun membentuk segitiga Pascal. Angka-angka ini juga muncul dalam kombinatorika, dimana
(keduanya memiliki nilai yang sama). Koefisien untuk setiap variasi n dan b dapat disusun membentuk segitiga Pascal. Angka-angka ini juga muncul dalam kombinatorika, dimana 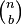 menunjukkan banyaknya kombinasi yang berbeda dari unsur b yang dapat dipilih dari suatu himpunan dengan unsur sebanyak n.
menunjukkan banyaknya kombinasi yang berbeda dari unsur b yang dapat dipilih dari suatu himpunan dengan unsur sebanyak n.
Contoh

Segitiga Pascal
Contoh paling dasar teorema binomial adalah rumus untuk x + y kuadrat
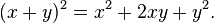
Koefisien binomial 1, 2, 1 muncul dalam pengembangan ini sesuai
dengan baris ketiga dari segitiga Pascal. Koefisien tingkat yang lebih
tinggi dari
x +
y sesuai dengan baris selanjutnya dari segitiga itu:
![\begin{align}
\\[8pt]
(x+y)^3 & = x^3 + 3x^2y + 3xy^2 + y^3, \\[8pt]
(x+y)^4 & = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4, \\[8pt]
(x+y)^5 & = x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 + 5xy^4 + y^5, \\[8pt]
(x+y)^6 & = x^6 + 6x^5y + 15x^4y^2 + 20x^3y^3 + 15x^2y^4 + 6xy^5 + y^6, \\[8pt]
(x+y)^7 & = x^7 + 7x^6y + 21x^5y^2 + 35x^4y^3 + 35x^3y^4 + 21x^2y^5 + 7xy^6 + y^7.
\end{align}](http://upload.wikimedia.org/math/2/8/a/28a6d79ecfecab5040d2b84fbd98f13f.png)
Perhatikan bahwa:
- Eksponen dari
 menurun hingga mencapai 0 (
menurun hingga mencapai 0 (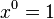 ) dengan nilai awal adalah n (n pada
) dengan nilai awal adalah n (n pada  ).
).
- Eksponen dari
 naik dari 0 (
naik dari 0 (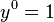 ) hingga mencapai n (juga n pada
) hingga mencapai n (juga n pada  ).
).
- Baris ke-n pada segitiga Pascal akan menjadi koefisien binomial yang dikembangkan (perhatikan bahwa puncaknya adalah baris 0).
- Untuk setiap baris, jumlah semua unsur (yaitu jumlah dari koefisien) sama dengan
 .
.
- Untuk setiap baris, banyaknya unsur sama dengan
 .
.
Teorema binomial dapat diterapkan ke eksponen dari binomial apapun. Contohnya,

Untuk binomial dalam pengurangan, teorema binomial dapat diterapkan dengan menggunakan tanda yang berlawanan pada suku berikutnya:
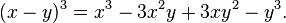
Contoh lain yang berguna adalah pengembangan akar
kuadrat berikut:


Distribusi binomial
Dalam teori probabilitas dan statistika, distribusi binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam n percobaan ya/tidak (berhasil/gagal) yang saling bebas, dimana setiap hasil percobaan memiliki probabilitas p. Eksperimen berhasil/gagal juga disebut percobaan bernoulli. Ketika n = 1, distribusi binomial adalah distribusi bernoulli. Distribusi binomial merupakan dasar dari uji binomial dalam uji signifikansi statistik.
Distribusi ini seringkali digunakan untuk memodelkan jumlah keberhasilan pada jumlah sampel n dari jumlah populasi N,pabila sampel tidak saling bebas (yakni pengambilan sampel tanpa pengembalian), distribusi yang dihasilkan adalah distribusi hipergeometrik, bukan binomial. Semakin besar N daripada n, distribusi binomial merupakan pendekatan yang baik dan banyak digunakan.
Contoh:
Sebagai contoh,sebuah dadu
dilempar sepuluh kali dan dihitung berapa jumlah muncul angka empat.
Distribusi jumlah acak ini adalah distribusi binomial dengan n = 10 dan p = 1/6.
Contoh lain, sebuah uang logam
dilambungkan tiga kali dan dihitung berapa jumlah muncul sisi depan.
Distribusi jumlah acak ini merupakan distribusi binomial dengan n = 3 dan p = 1/2.


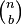 atau
atau  (keduanya memiliki nilai yang sama). Koefisien untuk setiap variasi n dan b dapat disusun membentuk segitiga Pascal. Angka-angka ini juga muncul dalam kombinatorika, dimana
(keduanya memiliki nilai yang sama). Koefisien untuk setiap variasi n dan b dapat disusun membentuk segitiga Pascal. Angka-angka ini juga muncul dalam kombinatorika, dimana 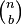 menunjukkan banyaknya kombinasi yang berbeda dari unsur b yang dapat dipilih dari suatu himpunan dengan unsur sebanyak n.
menunjukkan banyaknya kombinasi yang berbeda dari unsur b yang dapat dipilih dari suatu himpunan dengan unsur sebanyak n.
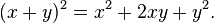
 menurun hingga mencapai 0 (
menurun hingga mencapai 0 (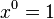 ) dengan nilai awal adalah n (n pada
) dengan nilai awal adalah n (n pada  ).
). naik dari 0 (
naik dari 0 (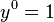 ) hingga mencapai n (juga n pada
) hingga mencapai n (juga n pada  ).
). .
. .
.
![\begin{align}
\\[8pt]
(x+y)^3 & = x^3 + 3x^2y + 3xy^2 + y^3, \\[8pt]
(x+y)^4 & = x^4 + 4x^3y + 6x^2y^2 + 4xy^3 + y^4, \\[8pt]
(x+y)^5 & = x^5 + 5x^4y + 10x^3y^2 + 10x^2y^3 + 5xy^4 + y^5, \\[8pt]
(x+y)^6 & = x^6 + 6x^5y + 15x^4y^2 + 20x^3y^3 + 15x^2y^4 + 6xy^5 + y^6, \\[8pt]
(x+y)^7 & = x^7 + 7x^6y + 21x^5y^2 + 35x^4y^3 + 35x^3y^4 + 21x^2y^5 + 7xy^6 + y^7.
\end{align}](http://upload.wikimedia.org/math/2/8/a/28a6d79ecfecab5040d2b84fbd98f13f.png)

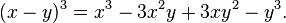

Tidak ada komentar:
Posting Komentar